| S-NAP/Field
for Windowsは、シールド領域のモーメント法解析エンジンを搭載したプレーナ回路用電磁界シミュレータで、L,C,Rトランジスタなどのような回路部品を混在させて解く事ができる新しいタイプのマイクロ波シミュレータです。かつて別々のシミュレーション問題とされていた回路シミュレーションと電磁界シミュレーションを統合して解く事により、回路要素を考慮した電流分布、電界分布などがシミュレーションでき、アクティブアンテナなどもいながらにして解析できます。換言すれば、モーメント法を用いた新しい回路解析手法と言えます。 |
| ● |
シールド領域、マルチレイヤーにおけるプレーナ回路をモーメント法で解析します。 |
| ● |
L、C、R、トランジスタなどの回路要素をモーメント法のインピーダンス行列と連立して解くことで、回路素子を混在した電磁界解析を行い、電流分布、Sパラメータ、雑音指数等を計算します。 |
| ● |
抵抗、インダクタ、キャパシタ、Sパラモデル、トランス、トランジスタ、コントロール電源、アイソレータ、サーキュレータなど40種以上の部品が混在可能です。 |
| ● |
レイヤー、ビアは無制限に使用でき、グランドビアおよび隣接する層間をビアで接続できます。 |
| ● |
シートリアクタンス、シートレジスタンスなど1つのレイヤで複数の導体プロパティを設定できます。 |
| ● |
アンテナ解析のための遠方界指向性パターンの3D表示、指向性利得のシミュレーションも可能です。 |
| ● |
3D表示による電流密度分布、タイムスイープによる位相表示がビジュアルに可能です。 |
| ● |
DXF、ガーバーファイルの入出力が可能です。
|
【原理】 |
| S-NAP/Fieldは、シールド領域のグリーン関数を用いた電界の積分方程式を、モーメント法を用いて解析する電磁界シミュレータです。簡単化のために2次元のみで概略原理を説明すると、図のようにシールドBOX内のあるZ位置におけるx-y平面状の(x’,y’)点に電流素J(x’,y’)がおかれた場合、同じZ位置における任意の点(x,y)には(1)式の電界が発生します。(1)式においてG(|)はダイアディックグリーン関数です。(1)式を数値計算にて解くためにJ(x,y)を既知の展開関数の線形結合と仮定し(2)式のように置き換えます。ガラーキン法を適用しField領域でもSource領域と同じ重み関数を用い内積をとると、最終的に(5)式の連立方程式が出来上がります。具体的にはパターンをサブセクションと呼ばれる小領域に分割し、それぞれのサブセクションに変数を割り当てます。サブセクションの電流はそのサブセクションのみで存在しそれ以外では0になるような展開関数を割り当てます。展開関数(重み関数)にはroof-top functionを用いています。(5)式を解くことでroof-topの屋根の高さが得られ、各roof-topの頂点を結ぶことでパターン全体の電流密度分布を得ることができます。 |
|
|
【特徴】 |
| 1. |
シールド領域のグリーン関数は(7)式のようにTE,TMモードの級数和となり初等関数による比較的簡単な形で表されます。このためSource/Field領域における4重積分を解析的に導出でき、数値積分を行う手法に比較すると積分誤差が極めて小さくなり高精度の解が得られる特徴があります。 |
| 2. |
S-NAP/Fieldは解析領域を完全なキャビティ状態にできます。多くのマイクロ波回路はシールドBOXに納められますので、BOXの影響なども考慮する必要があります。この手法ではBOXの影響も考慮できるほかBOX共振周波数なども解析が可能となります。 |
|
|
|
| 3. |
S-NAP/Fieldはシート電流を変数としており変数は導体表面にしか設定されません。このためFEM(有限要素法)やFD-TD法、TLM法など空間まで離散化する手法と比較するとマトリックスはコンパクトとなり、空間領域が増えてもマトリックスサイズは変化しないという特徴があります。また、空間まで離散化する手法では極端に薄いレイヤなど寸法変化が大きな場合や、誘電率が大きく変わるような場合は精度の高い離散化が難しくなり誤差の要因となることがありますが、境界部分でしか変数設定を行わないモーメント法ではこのような誤差はほとんど発生しなくなります。 |
| ※ |
ここで比較対象として説明したFEM(有限要素法)やFD-TD法、TLM法の特徴は一般的な場合であり、特定のシミュレータを対象としたものではありません。 |
|
【対象問題】 |
| 電磁界シミュレータは解析手法により得意とする問題が異なってきます。S-NAP/Fieldは、グリーン関数を導出する際の境界条件としてシールドBOX内に積み上げられた誘電体レイヤを仮定しています。したがってこのような構造となる多層基板回路が最も適合する問題となります。さらに部品実装機能を有するため、実装状態の多層基板問題まで適用可能となります。 |
|
|
【高速スイープAWE法】 |
| S-NAP/Fieldのような周波数領域の解析ソルバは、基本的には1周波数ずつ解析を行っていきますが、細かい特性を得ようとしてサンプル数を増やそうとすると長時間を要することになります。AWE(Asymptotic Wave Evaluation)法は、高速にスイープする手法の一つで、解の漸近方程式を得ることである帯域内の解を一気に計算する手法です。漸近方程式にはPadeの有理多項式を用います。この手法は展開ポイント(k0)での逆行列しか必要としないので、マトリックス分解の時間を大幅に軽減できるという特徴があります。図のフィルタ特性の場合、連立方程式を計算しているのは中心周波数の2.5GHzだけで、それ以外の周波数での特性は、有理多項式から得ています。この回路例の場合、わずか1点の解にもかかわらず真値に非常に近い特性であることがわかります。S-NAP/Fieldにはこの特性を利用したスケッチモードがあります。スケッチモードはその名の通り「概要」を求めるモードですが、フィルタやアンテナなどの中心帯域の特性を高速に得ることができますので、イメージを崩すことなく設計を行うことができます。 |
 |
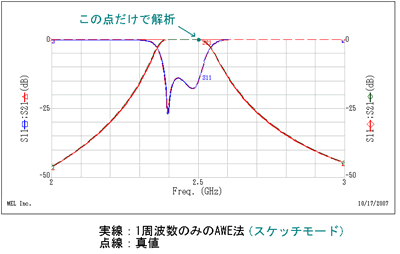
※回路の特性によりAWE法の整合率は異なります。 |
|
【導波管励振モード】 |
S-NAP/Fieldで用いられるシールド領域のグリーン関数は導波管と同じであるため、図のようにBOXの上下を導波管ポートとすることで導波管問題が解析可能で、E面H面にかかわらず任意形状の窓導体を解析可能です。ただし無厚導体ですので、厚みのあるアイリスのような場合は導体を重ねて厚みを持たせる必要があります。
導波管ポートを窓導体までオフセットし、Fパラメータを求めることで窓導体の等価リアクタンス特性を得ることができます。また導波管ポートから励振されたドミナントモード(TE10)は、窓導体にぶつかりモード変換が生じ、高次モードやTMモードに変換されます。これらのモードに対応する多線状線路にポートを設けておけばモード変換マトリックスを求めることができます。その他の用途として、この機能は同軸-導波管変換の解析や導波管励振アンテナなどの解析にも応用が可能です。 |
|
|
【入射波励振モード】 |
入射波励振モードは、アンテナにある電界強度の波が到来した場合に、どれぐらいの電圧がポートに誘起されるかを解析するモードです。部品実装機能やハーモニック・バランス機能などと合わせて解析をすることで、受信アクティブアンテナの特性やレクティナアンテナの特性などを解析することができます。
入射波励振モードの原理は導波管ポートと同じです。図のようにBOX境界を自由空間に接続し、この片側の開口部に入射波が到来していると考えます。したがって正確に言えばアンテナ面ではなくて開口面での電界強度規定になります。開口部にあたった入射波はTE10モード、TE01モード、TM11モードに変換されBOX内を伝播すると考えられますので、これらの波が伝播している状態でアンテナポート部の電圧を求めると入射波に対する誘起電圧が得られます。 |
|
|
【ハーモニック・バランス解析法の実装】 |
ハーモニック・バランス法は、回路解析において非線形解析を行う場合に用いられる手法の一つで、周波数領域での非線形解析を行うものです。 特徴としては、
| ● |
周波数差の大きな2信号がある場合でも容易に解析が可能である。 |
| ● |
定常応答解が得られるため、高周波非線形回路解析に向いている。 |
などが上げられます。S-NAP/Fieldはこの手法を実装し、アクティブデバイスが混在している回路の非線形特性を解析することができます。また入射波解析と併せて用いれば受信用のアクティブアンテナやレクティナアンテナなどの解析も行えます。
通常このような機能がない場合でもポートからの励振だけであれば、素子端子にポートを取り付け、NポートのSパラデータを電磁界で求めてから回路シミュレータでハーモニック・バランスを実行することで、面倒ですが解を得ることは可能です。しかし入射波による励振の場合には非常に難しくなりますので、S-NAP/Fieldの入射波励振+ハーモニック・バランスの組み合わせはアクティブアンテナにとって強力なツールになると考えられます。
|
|
|
【コンボリューション・トランジェント解析法の実装】 |
| コンボリューション・トランジェント法は、回路中にSパラメータデバイスや伝送線路のように素子特性に周波数分散性がある場合、そのような素子を含めて時間領域から過渡応答特性を求める手法です。周波数分散性素子のインパルス応答を求め、畳み込み積分を行いながら応答特性を解析していきます。S-NAP/Fieldはこの手法を実装し、電磁界解析と併せて過渡応答を求めることができます。S-NAP/Fieldはトランジェント解析が選択されると、最初にスイープ時間からコンボリューションに必要なスペクトルを計算します。次にそれらのスペクトルでモーメント法を実行します。電磁界解析終了後それらのデータをもとに指定された信号における過渡応答特性を畳み込み積分法を用いて計算します。非線形素子が実装されている場合も可能です。この機能はEMC問題に適用できます。
|
|
|
|

